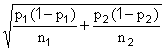 .
.When reading political polls, remember that the margin of error in an estimate of the “gap” between the two leading candidates is roughly twice as large as the poll's reported margin of error, and the margin of error in the estimated “change in the gap” from one poll to the next is nearly three times as large as the poll's margin of error.
WASHINGTON (Reuters - 09/09/00) - A new Newsweek poll on Saturday showed Vice President Al Gore maintaining a strong lead over Texas Gov. George Bush in the presidential race, but a CNN/USA Today survey found the candidates virtually tied.
According to the Newsweek poll, Democratic nominee Gore leads Republican nominee Bush 47 percent to 39 percent among registered voters, with Green Party candidate Ralph Nader at 3 percent and Reform Party candidate Pat Buchanan at 1 percent.
Among likely voters, Gore led Bush 49 percent to 41 percent, the same margin as among registered voters.
The poll was conducted by Princeton Survey Research Associates Sept. 7-8 among 756 registered voters, including 595 who said they were likely to vote in the election.
The margin of error was 4 percentage points for the survey of registered voters and 5 percentage points for likely voters.
Comment: 1/√756 = 3.64%, and 1/√595 = 4.10% . PSRA conservatively rounds these up to the next integer percentage. Does the 4% margin of error mean that Buchanan might plausibly be drawing the support of 5% of the voters? No. Carefully computing the margin of error in the estimate of his support level, we find it to be 1.96 √[(0.01)(0.99)/756] = 0.71% . Remember that 1/√n is only an upper bound for the actual margin of error (at the 95%-confidence level), and that, while close to the actual margin of error for estimates near 50%, is substantially greater than the actual margin of error for more extreme proportions.
A week ago, the Newsweek poll of registered voters put Gore's lead at 49 percent to 39 percent over Bush, suggesting the race has tightened slightly over the past week.
Comment: The commentary at the end of this article[2] shows that the margin of error in using 47% - 39% = 8% as an estimate of the “gap” is roughly double the reported margin of error in the poll results, i.e., roughly 8%. There’s strong evidence that Gore is ahead, but we can’t trust the estimate of the size of the gap very much. Assuming that the previous week’s poll was based on a sample of comparable size, we estimate the decrease in Gore’s lead to be (49%-39%) – (47%-39%) = 2%. However, the margin of error in this “change in differences” is actually about 41% larger[1] than the 8% margin of error in the estimate of each separate gap, i.e., is more than 11%! These poll results actually provide no meaningful evidence that the race has tightened.
Unlike Bush, Gore has held onto much of the surge in popularity that both candidates enjoyed following their parties' nominating conventions.
Still, a separate CNN/USA Today poll of 952 registered voters Sept. 6-8 showed a much tighter race.
Gore led Bush 46 percent to 43 percent among registered voters. But Bush led Gore 46 percent to 45 percent among the 675 respondents who said they were likely to vote.
The results were within the margin of error of 3 percent for the registered voters survey and 4 percent for the likely voters poll. Gallup conducted the survey.
Fifty-four percent of the registered voters in the Newsweek survey brushed off Bush's recent off-color comment about a New York Times reporter by saying it made no difference in their opinion of him.
But 27 percent said they now had a less favorable opinion of Bush because of the remark, which was caught by an open microphone at a campaign event.
Thirty-three percent of the registered voters said Bush was more to blame for problems in reaching an agreement on the timing and location of presidential debates. Twenty-seven percent in the Newsweek poll said it was mostly Gore's fault.
More voters continue to think Gore would do a better job on key issues such as health care, Social Security, education and taxes, the Newsweek poll found.
But Bush still edges Gore on leadership qualities, though more registered voters see Gore as honest and ethical, and intelligent and well-informed, the survey found.
Meanwhile, a batch of state polls showed Bush with a wide lead in Kentucky and Indiana, but in a virtual dead heat with Gore in the key swing state of Ohio.
The polls for ABC-affiliate WCPO-TV by Survey/USA of 500 likely voters in each state had Bush leading Gore by 52 percent to 38 percent in Indiana, 51 percent to 42 percent in Kentucky, and 48 percent to 44 percent in Ohio.
The remaining 10 percent in Indiana, 7 percent in Kentucky, and 8 percent in Ohio were split among candidates from other parties and respondents who were undecided.
Pollsters said Bush's 4 percent margin in Ohio was within the 4.5 percent margin of error, making the race in the Buckeye State, an important battleground in the contest, a dead heat.
The Texas governor has widened his margin over the vice president in Ohio since a poll by Survey/USA soon after the Democratic National Convention last month, which had Bush ahead 47 percent to 45 percent.
In Kentucky, Gore had reduced Bush's margin from 15 percent to 9 percent since a Survey/USA poll released two weeks ago.
While Indiana has been conceded to Bush by most political strategists, Ohio and Kentucky have been regarded as up for grabs in the decisive Electoral College tallies, with each candidates devoting considerable campaign time to both states.
And in Illinois, a Chicago Sun-Times/Fox News Chicago poll of 600 Illinois voters showed Gore leading Bush 44 percent to 40 percent, but Gore's apparent lead was eclipsed by the poll's margin of error of plus or minus 3.9 percentage points.
Comment: 1.96 √[(0.4)(0.6)/600] = 3.92% . The margin of error in each of the two estimates is at least this much, so it appears the Sun-Times and Fox are aggressively rounding their margins of error down. This is not good. Fortunately, their conclusion is correct, since the lead is definitely “eclipsed” by the actual margin of error of roughly twice their 3.9%, i.e., nearly 8% in the estimate of the difference in support levels.
This article, like most articles reporting poll results during the campaign season, reports estimates of the proportion of the electorate favoring each of the candidates. Each such estimate, on its own, is somewhat subject to sampling error, and the margins of error for the various estimates are correctly reported.
But are these estimates really the primary focus of the article? If the article simply reported that, if the election were held today, Gore would draw 46% of the vote, would any reader find this interesting? Of course not. It’s the comparison between the levels of support for Gore and Bush that is actually of interest. The writer of the article clearly recognizes this, continually referring to “margins,” i.e., to the differences between the (estimates of the) proportions of voters favoring the two main candidates.
How much can we trust these estimates of the differences between proportions? If, perchance, sampling error leads to an overestimate of Bush’s support, then, perforce, it must at the same time lead to an underestimate of some other candidate’s – most likely, Gore’s – support. This doubled effect suggests that the margin of error when estimating the difference in support for the two leading candidates is roughly twice the margin of error in estimating a single candidate’s level of support. The following analysis shows that our intuition is justified: A decent rule-of-thumb is to double the margin of error reported in a news article when looking at differences between the estimated voter support of the two leading candidates.
[1] Let p1 and p2 be proportions (i.e., fractions) of two distinct populations. Let C represent the random variable which results from estimating each using samples of size n1 and n2 , and then computing the difference between the two estimates. C is an unbiased estimator of p1- p2 ; it is approximately normally distributed, and its variance is the sum of the variances of the separate estimators of p1 and p2 , i.e.,
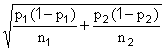 .
.Clearly, if both separate estimates have roughly the same margin of error, then the margin of error in estimating the difference between the two, using independent samples, is roughly √2 times either original margin of error, or roughly 41% greater.
[2] Assume that, across the population of voters being studied, a fraction p of the voters currently support Gore, and a fraction q currently support Bush. Let us randomly sample n voters, and encode the preference of voter i as
| 1, | if the voter supports Gore | |
| Xi = | 0, | if the voter supports neither Gore nor Bush |
| -1, | if the voter supports Bush |
Using this encoding, D = (X1 +...+ Xn) / n will be the difference between the proportion of voters supporting Gore, and the proportion supporting Bush.
It is straightforward to show that E[Xi] = p-q , and Var[Xi] = (p+q) – (p-q)2. From this it follows that E[D] = p-q, i.e., D is an unbiased estimator for the difference between the proportions. Furthermore,
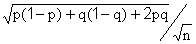
Replacing p and q with the estimates we derive for them from the sample data yields the standard error of the difference between support levels. Note that when the estimates are both near 50%, the quantity within the square-root calculation in the numerator is roughly four times as large as is either of the first two terms alone, and therefore the standard error of the difference will be roughly twice as large as the standard error of either individual proportion. This justifies the rule-of-thumb proposed above.