Every statistical procedure consists of three specifications: how to collect sample data, how much to collect, and what to do with that data. The first two of these – the “how” and “how much” specifications – together determine a sampling procedure.
The foremost objective when deciding how sample data will be collected is to avoid sampling bias, i.e., the systematic omission (or under-representation) of some specific group of individuals from the data-collection process. The primary line of defense against sampling bias is good judgment, based on prior experience dealing with the population being studied. No subsequent statistical analysis of data collected in a biased fashion will reveal the bias (and all statistical analysis begins with the assumption that the sample data has been collected in an unbiased manner).
The goals of sampling are to use a procedure that is likely to yield a “representative” sample of the population as a whole (i.e., to limit exposure to sampling error), while holding down sampling costs as much as possible. From a narrow perspective, if we limit ourselves to one particular way of collecting data, we face a clear trade-off: Large samples limit our exposure to sampling error, but are very costly. However, if we broaden our perspective to allow for different data-collection methods, we find that sometimes one method can involve both less exposure to sampling error and lower costs than another.
The three most-commonly-used methods for collecting sample data (when the goal of a study is to estimate means and proportions) are simple random sampling, stratified sampling, and cluster sampling.
Simple random sampling. Observations are obtained by sequentially selecting individuals from the population, and each time a selection is made, all “available” individuals have equal chances of being selected. Simple random sampling has two distinct flavors: Sampling with replacement leaves individuals already selected available to be selected again, while sampling without replacement removes previously-selected individuals from the population before subsequent selections (and thus avoids the possibility of the same individual appearing in the sample more than once).
If all the members of the population are directly at hand (for example, if the population is all the units of product in a truck), or a list of all the members of the population is available (for example, all the subscribers to a magazine), then simple random sampling is not difficult to implement. In practice, such sampling is almost always done without replacement. The only reason sampling with replacement is discussed is because it is a somewhat easier procedure to analyze mathematically.
However, many times the members of the population are scattered about (in space or in time), and no list exists. For example, one might wish to study the population of all tourists visiting Chicago during the summer. In such a case, data is frequently collected using systematic sampling. One finds a location past which members of the population “flow,” and selects from the flow (for some k) every k‑th encountered member of the population, until a sample of the desired size is obtained. Unless members of the population are being encountered in some periodic fashion, or some special class of members is likely to be underrepresented in the encounters that occur while the sample is being drawn, this method of sampling works as well as (and is interchangeable with) simple random sampling, and is usually less expensive to carry out.
Stratified sampling. This involves drawing a specified portion of the sample (at random) from each (and every) of several distinguishable groups of members (i.e., strata) of the population. Typical reasons for this are to control for expected differences between the groups (for example, sampling from the pools of men and women separately, in proportion to their representation in the population, if we expect the characteristic being studied to be distributed differently for men than for women). When the population does contain important differences between groups, a stratified sample may yield estimates that are less subject to sampling error than estimates derived from a random sample of equal size. The drawback is that stratified sampling can be somewhat more expensive than simple random sampling, on a per-individual-sampled basis, since data must be collected and tracked separately for each stratum.
Cluster sampling. This involves dividing the population into “clusters” (blocks in a city, or each day’s sales slips over a period of several weeks), randomly choosing some of the clusters, and then sampling individuals from each chosen cluster. If carefully done, this can generate a representative sample with less expenditure of effort than is involved in using a method that could require selecting members from every cluster (visiting all blocks, or handling every day’s slips). The drawback is that, to the extent that the variation among individuals within clusters is less than the overall population variation, cluster sampling yields estimates somewhat more subject to sampling error than does simple random sampling of the same aggregate number of individuals from the population.
The table below summarizes the distinctions between these three procedures:
| stratified | simple random | cluster | |
|---|---|---|---|
| cost / person sampled | high | medium | low |
| sample size required to achieve specified precision | low | medium | high |
| appropriate circumstance for use | when the population divides itself naturally into homogeneous “strata,” with substantial interstratum differences | when the population has no natural divisions | when the population divides itself naturally into geographic “clusters,” and each cluster is nearly as heterogeneous as is the entire population |
| procedure | simple random sampling within every stratum, yielding estimates for all strata; final estimate is size-weighted average of stratum estimates | simple random sampling to choose some clusters, followed by simple random sampling within each selected cluster; final estimate is size-weighted average of cluster estimates |
Beyond these three standard procedures for estimating means, a few others warrant brief comment.
Randomized response surveys. A method of growing popularity for conducting surveys on “sensitive” topics such as sexual habits, drug use, and tax evasion, such a survey asks individuals to determine privately whether to answer truthfully or to lie (e.g., “Flip a coin twice: If heads come up both times, answer truthfully, else lie.”). While individual responses give little information about the individual’s behavior, sufficiently-large samples provide very accurate estimates of the distribution of behavior within the population.
Interventionary sampling. An example of this is the use of tagging to estimate wildlife populations. Another example is the purposeful introduction (“seeding”) of bugs into computer software prior to validation testing; the ratio of discovered seeded bugs to discovered actual bugs, together with the proportion of seeded bugs discovered during testing, is used to estimate the number of actual bugs remaining after testing is complete.
Finally, one sometimes encounters studies involving “judgment sampling.” A non-statistical and potentially hazardous (in terms of exposure to bias) means of obtaining a sample, this method involves using one’s instincts and past experience to guide the choice of a representative sample. It is sometimes used in selecting localities for test-marketing a product.
Simple random sampling: Assume that a study is to be carried out, using simple random sampling to estimate a population mean. For example, subscribers to a magazine are to be sampled in order to estimate the mean dollar amount (across all subscribers) spent on furniture in the previous twelve months.
The critical specification needed to determine the scale of a study is the target margin of error, that is, the margin of error the estimation procedure should be subject to. There is little science to help us here: The target margin of error should be small enough that the ultimate decision-maker will be able to reach a firm decision after receiving the estimate and conducting the appropriate decision and risk analyses. Subject to this condition, the target margin of error should be as large as possible, in order to minimize the cost of the study. Say, for example, we wish our estimate of the mean amount spent by the magazine’s subscribers to be subject to a margin of error (at the 95%-confidence level) of $25.
Knowing that the margin of error in our procedure will be ![]() , we need simply solve the equation
, we need simply solve the equation
for n in order to find the sample size required in order to have the desired level of precision in the estimation procedure. Unfortunately, there is an obvious problem: Before the study is completed, we don’t know the sample standard deviation s.
This problem is typically resolved in one of two ways. If historical data exists (for example, if a similar study was done six months ago, and we don’t think that the net variability across the population has changed much since then) which suggests roughly how large s will turn out to be, this rough value can be used in place of s for planning purposes.
If no such rough estimate of s is available, then a pilot study involving a small number of individuals can be conducted in order to come up with an estimate of s, and therefore an estimate of the required size of the full study.
When estimating proportions, we can exploit the fact that the margin of error (at the 95%-confidence level) in the estimate of a proportion will always be somewhat less than 1/√n. For example, if we want our estimate to have a margin of error of no more than 4%, a sample size of 625 will assuredly suffice.
Stratified sampling: Assume that the population (of size N) is divided into k strata (of
sizes N1 ,..., Nk ). If samples of sizes n1 ,..., nk
are drawn from the strata, yielding stratum sample means and sample standard deviations of ![]() and
s1,...,sk , then a 95%-confidence interval for the resulting estimate of the
population mean will be
and
s1,...,sk , then a 95%-confidence interval for the resulting estimate of the
population mean will be
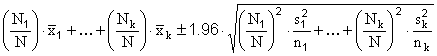 .
.In order to plan the size of the study, the formula for the margin of error is set equal to the
target margin of error, and the resulting equation is solved for n1 ,..., nk
. Once again, historical data or a pilot study is required to determine “planning
values” for s1,...,sk . While many different combinations of stratum
sample sizes will satisfy the equation, the combination that minimizes the sum of the sample sizes
(i.e., which minimizes the total sampling effort) will set the stratum sample sizes to be
proportional to the quantities ![]() .
.
Cluster sampling: The formula for the margin of error in an estimate derived via cluster sampling is quite complex. In essence, the formula uses the within-cluster variability amongst individuals, and the between-cluster variability, to estimate how much additional variability exists in the clusters from which data was not collected. Still, the approach of using historical data or data from a pilot study to determine the number of clusters from which to collect data, and how much data to collect from within each selected cluster, parallels the approach used in stratified sampling.